数値積分法と刻み幅について
Fortran90でリチャードソン補外とか
大学のFortranの演習課題でやったので、メモとして載せておきました。いちおう動きましたが、中身は保証しませんよw
(課題)
(1) 数値微分の時と同様に N を大きくしていった時に、数値積分の精度がどうなるか考察せよ。
(2) Richardson補外で数値積分の精度が改善されることを確認せよ。
(解答)
(1)
以下のようなプログラムを作成してf(x)=e^xを範囲[0,1]で数値積分と解析的な解の誤差を比べたところ刻み数nと積分の誤差は図1のようになった。
なお、細い誤差の議論をするため、(1)(2)ともにすべて倍精度計算を用いた。
*******************************************************************
program integ1
implicit none
real(8) a,b,h,x,s,s0
integer(4) n,i,k
character(len=20) fname
write(*,'(a,$)') 'file name ?(len=20) '
read(*,*) fname
open(10,file=fname)
do k=1,25
n=2**k
a=0.0d0
b=1.0d0
h=(b-a)/real(n)
s=(exp(a)+exp(b))/2.0d0
do i=1,n-1
x=a+real(i)*h
s=s+exp(x)
end do
s=s*h
s0=exp(1.0d0)-1.0d0
write(10,'(e20.10,e20.10)') real(n),abs(s-s0)
end do
close(10)
end program integ1
*********************************************************************
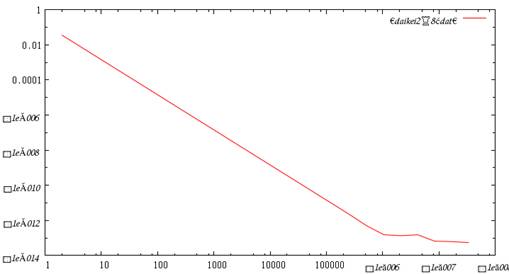
図1 横軸は刻み数n、縦軸は誤差、両方とも対数スケールで表示
刻み数が10^6程度で誤差が10^(-12)程度で収束している。数学的には刻み幅を無限に細かくすれば誤差は0に限りなく近づくが、数値計算では刻み幅を小さくすることによる誤差の現象という数学的な効果と、コンピュータで扱える数値の精度による誤差の蓄積とが拮抗する場所で収束が起こってしまう。
(2)
(1)と同じ積分計算に対して、Richardson補外(リチャードソン補外)
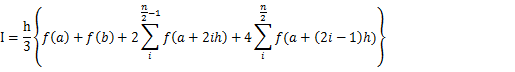
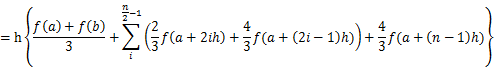
を用いた数値積分を以下のようなプログラムを作成して実行した。
********************************************************************************
program integ1
implicit none
real(8) a,b,h,x,t,s,s0
integer n,i,k
character(len=20) fname
write(*,'(a,$)') 'file name ?(len=20) '
read(*,*) fname
open(10,file=fname)
do k=1,25
n=2**k
a=0.0d0
b=1.0d0
h=(b-a)/real(n)
s=(exp(a)+exp(b))*h/3.0d0
do i=1,n/2-1
x=a+2.0d0*real(i)*h
t=a+(2.0d0*real(i)-1)*h
s=s+(2.0d0/3.0d0*exp(x)+4.0d0/3.0d0*exp(t))*h !n/2-1まで和をとる
end do
s = s + (4.0d0/3.0d0*exp(a+(n-1)*h))*h !tのn/2の分を足す
s0=exp(1.0d0)-1.0d0
write(10,'(e20.10,e20.10)') real(n) , abs(s-s0)
end do
close(10)
end program integ1
******************************************************************************
この結果を(1)と同様に数値積分と解析的な解の誤差を比べたところ刻み数nと積分の誤差は図2のようになった。
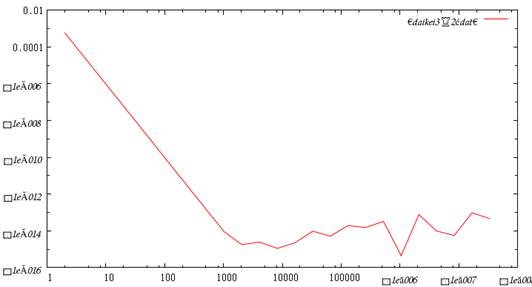
図2 横軸は刻み数n、縦軸は誤差
収束する積分値は台形公式よりも誤差が2桁程度小さくなった上、収束する際の刻み数が台形公式のn~106に比べてリチャードソン補外によりn~103となっており、3桁小さいうちに収束していることがわかる。すなわち、補外によって誤差の大きさだけでなく収束性も改良されていると言える。