4次精度、6次精度の数値微分
大学のFortranの演習課題でやったので、メモとして載せておきました。いちおう動きましたが、中身は保証しませんよw
問題
(1)
f(x+2h), f(x+h), f(x-h), f(x-2h) を使って4次精度の微分公式を,
f(x+3h), f(x+2h), f(x+h), f(x-h), f(x-2h), f(x-3h) を使って 6次精度の微分公式を導出せよ。
(2) 4次精度、6次精度の微分公式を使って数値微分を実行し、最適な刻み幅hの大きさを評価せよ。
(3) 倍精度の実数を使った数値計算を行い、微分精度がどれ程向上するかを評価せよ。
解答
(1)
・4次精度の数値微分の導出
![]()
![]()
の2つのテーラー展開を使う。これらについて3階微分までの項をとり、以下のように変形する。
![]()
![]()
これらから![]() を消去して、整理すると、
を消去して、整理すると、
![]()
となり、これが4次精度の数値微分の式となる。
6次精度の数値微分の導出
4次精度で用いた2つのテーラー展開に加えて、以下のテーラーも用いる。
![]()
3つの式について、4次精度の時と同様の式変形を、今度は5階微分までについて行う。
![]()
![]()
![]()
これらから
![]() と
と
![]() を消去して、
を消去して、
![]()
これが6次精度の数値微分の式となる。
(2) Fortran90で以下のようなプログラムを組んで計算を行う。
・4次精度
program main
implicit none
real x,h
real df,df0
integer n
character(len=20) fname
write(*,'(a,$)') 'x ? '
read(*,*) x
write(*,'(a,$)') 'file name ? '
read(*,*) fname
open(10,file=fname)
do n=0,20
h=1.0/(2.0**real(n))
style='color:red'>df=(2*sin(x+h)/3-2*sin(x-h)/3-1*sin(x+2*h)/12+1*sin(x-2*h)/12)/h
df0=cos(x)
write(10,'(2e15.8)') h,abs(df-df0)
end do
close(10)
end
program main
この計算の結果を.xls形式で出力し、Excelで対数グラフにした。この結果から、h=1.56×10-2という値のとき、誤差が最小で 2.98×10-7となることがわかった。
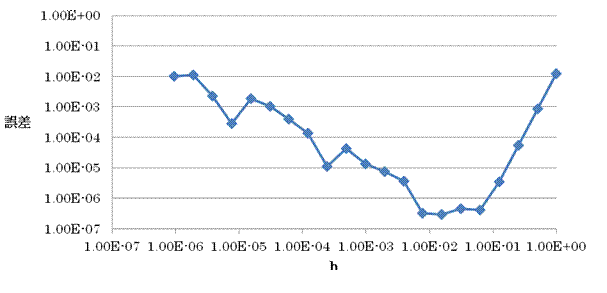
・6次精度
4次精度と同様のプログラムを組んで計算を行う。
program main
implicit none
real x,h
real df,df0
integer n
character(len=20) fname
write(*,'(a,$)') 'x ? '
read(*,*) x
write(*,'(a,$)') 'file name (len=20)? '
read(*,*) fname
open(10,file=fname)
do n=0,20
h=1.0/(2.0**real(n))
df=(3*sin(x+h)/4-3*sin(x-h)/4--3*sin(x+2*h)/20+3*sin(x-2*h)/20+sin(x+3*h)/60-sin(x-3*h)/60)/h
df0=cos(x)
write(10,'(2e15.8)') h,abs(df-df0)
end do
close(10)
end
program main
この計算の結果を.xls形式で出力し、Excelで対数グラフにした。この結果から、h=1.25×10-1という値のとき、誤差が最小で 1.79×10-7となることがわかった。この誤差の値は 4次精度の時よりも小さい。
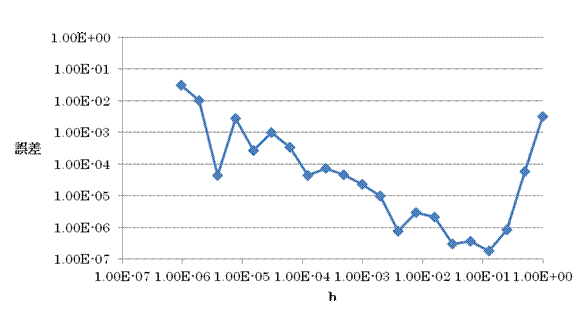
(3)
(2)で示した 4次精度、 6次精度のプログラムをともに、
real x,h
real df,df0
となっている部分を、倍精度実数の
double precision x,h
double precision df,df0
に変更して再度計算を行い、Excelでグラフを作成した。
・4次精度
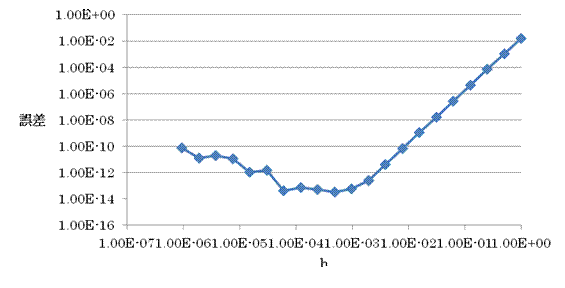
・6次精度
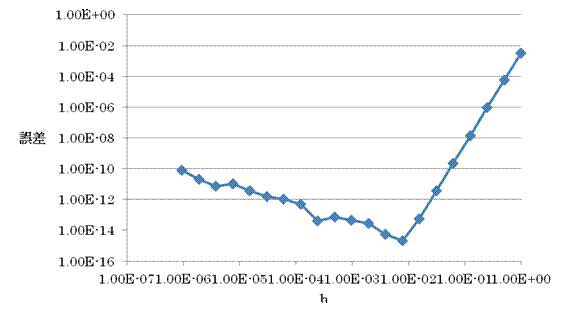
それぞれ、4次精度のときh=4.88×10-4で誤差は最小の3.19×10-14に、6次精度のときはh=7.81×10-3で誤差は最小の2.22×10- 15となる。倍精度実数を用いることにより、誤差の桁が倍近く小さくなったことがわかる。また、最適な刻み幅hも倍近く小さくなり、用いる実数の精度がよくなったことから、微小量の刻み幅を小さくすれば誤差が小さくなるという直感的なアナログの数学が効果を表す結果となった。