大学の授業で数値シミュレーションをFortran90でやるというものがあったので作ってみました。動機としては、鉱物趣味としてこういった結晶集合体に興味があったというのもありますし、高校の頃に化学の先生と少し自由研究していた結晶集合体に関する話があったので、それを思い出してやってみようということになりました。
プログラミングは右も左も分からない全くの初心者としてFortranを大学の授業ではじめたのでキッタナイコードでザコみたいな計算してますがw、大目に見てやってくださいw 最後に、ちゃんとした最新の研究についてリンクしておきましたので、興味ある方はゼヒ見てみて下さい。
・結晶成長と形態Morphology
以下の『結晶―成長、形、完全性
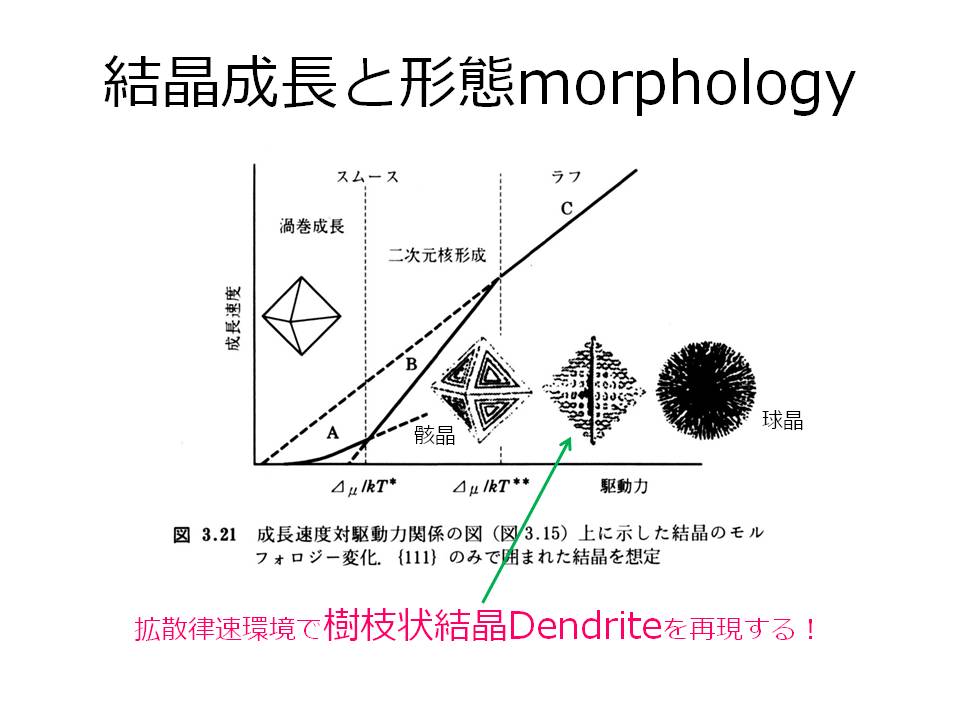
さらに、溶液成長や気相成長といった希薄環境(融液成長よりも結晶成長の材料物質に乏しい環境)では、樹枝状結晶になるには拡散律速の支配であることが知られています。今回は、この律速過程のみを考えた第一次近似によって、樹枝状結晶の成長をFortran90で再現してみました。
ちなみに、気相成長の樹枝状結晶の代表例としては”雪の結晶”、溶液成長の樹枝状結晶の代表例としては塩化アンモニウム、融液成長ではトタンの表面構造などが挙げられます。
・プログラムの設定
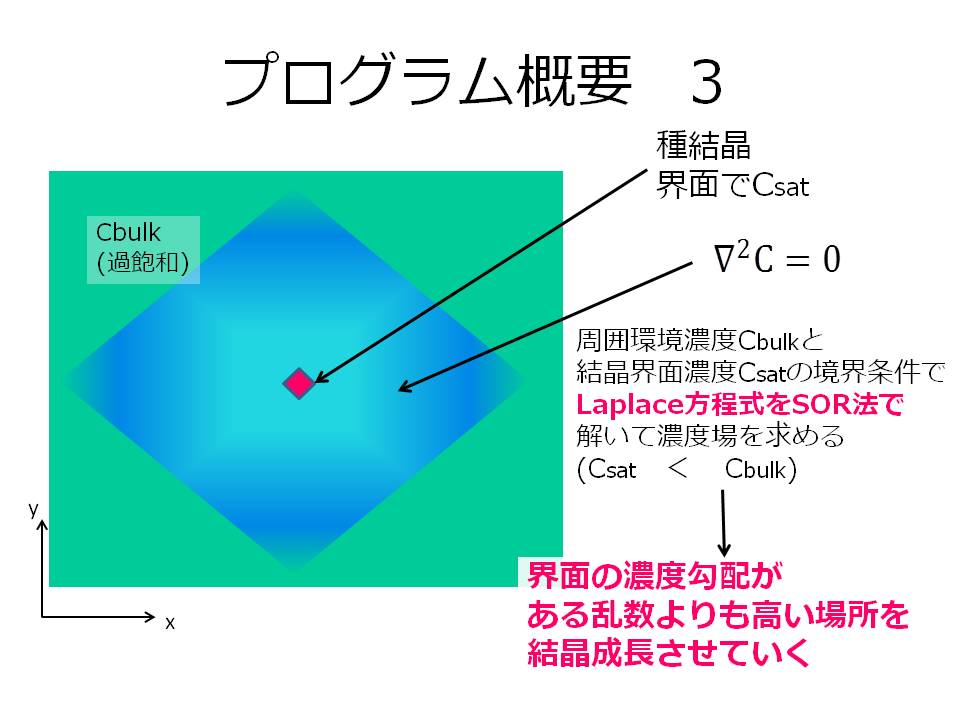
ネットで探してみて、簡単そうなのでこれに従ってやってみました。ただし、僕の技量では三角格子点を設定できないので、今回は普通のxy2次元平面で、ちょうど塩化アンモニウムの樹枝状結晶成長のような形でやりました。
上の2枚の画像で示したような設定の元、下の画像のようなイメージで濃度場の決定と結晶成長する格子点の決定、さらにデータの書き込みを繰り返すプログラムを作りました。
以下に汚いプログラムですが、作ってみたものを載せます。
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
program main
implicit none
! ◆変数の設定
integer x,y,t,iter
integer,parameter:: tmax=80 ! 実験時間＝反復回数t＝1～80
integer,parameter:: xmax=199 ! x,y 座標(1,1)～(199,199)
integer,parameter:: ymax=199
integer,dimension(xmax,ymax,tmax+1) :: S ! S=0,1 その格子点が結晶してるか
real*8,dimension(xmax,ymax,tmax):: C,gC ! 濃度C(x,y,t)と濃度勾配∇C(x,y,t)
real*8 Cnew,dC,dCmax,gCmax
real,parameter:: Cbulk=13000.0 ! 溶液のバルク濃度
real,parameter:: Csat=10000.0 ! 飽和濃度(溶解度) ※Csat < Cbulk
character(len=20) fname*128
! 場の初期設定(t=1) (100,100)に種結晶を置く
Do 2 x=1,xmax
Do 3 y=1,ymax
S(x,y,1)=0
S(100,100,1)=1
3 Continue
2 Continue
! ★判定の繰り返し
! 「濃度場決定→結晶化判定」の繰り返し
Do 99 t=1,tmax
Do 10 x=1,xmax
Do 11 y=1,ymax
C(x,y,t)=Cbulk
11 Continue
10 Continue
! 反復計算 ラプラス方程式(SOR法 加速係数omega=1.8とかで)
Do 19 iter=1,8000
dCmax=0.0
Do 20 x=2,(xmax-1)
Do 30 y=2,(ymax-1)
if (S(x,y,t)>=1 .or. S(x-1,y,t)>=1 .or. S(x+1,y,t)>=1 .or.
S(x,y-1,t)>=1 .or. S(x,y+1,t)>=1) then
C(x,y,t)=Csat ! ※表面張力の効果入れる式はここでいじくる
else if (y>=x+99 .or. y>=299-x .or. x-99>=y .or. 101-x>=y)
then ！ Cbulkの境界の移動とかはここで設定
C(x,y,t)=Cbulk
else
Cnew=0.25*(C(x+1,y,t)+C(x-1,y,t)+C(x,y+1,t)+C(x,y-1,t))
dC=Cnew-C(x,y,t)
dCmax=max(abs(dC),dCmax)
C(x,y,t)=C(x,y,t)+1.8*dC
end if
30 Continue
20 Continue
if (dCmax<1.0e-7) exit
19 Continue
! ◆結晶成長の判定
! ∇C=gC(x,y,t)の設定
! 0から1までの一様乱数の発生
do 40 x=2,(xmax-1)
do 45 y=2,(ymax-1)
if (S(x,y,t)>=1) then
gC(x,y,t)=0 ! 結晶になったところは0に
else if(S(x-1,y,t)>=1 .or. S(x+1,y,t)>=1 .or. S(x,y-1,t)>=1
.or. S(x,y+1,t)>=1 ) then
gC(x,y,t)=sqrt((C(x,y,t)-C(x-1,y,t))**2+(C(x,y,t)-C(x+1,y,t))**2+(C(x,y,t)-C(x,y-1,t))**2+(C(x,y,t)-C(x,y+1,t))**2)
else
gC(x,y,t)=0 ! 界面以外は0に
end if
45 continue
40 continue
! 勾配の最大を選ぶ
do 50 x=1,xmax
do 55 y=1,ymax
gCmax=max(gC(x,y,t),gCmax)
55 Continue
50 Continue
! 結晶してる点を次のtに引き継ぎ
do 160 x=1,xmax
do 165 y=1,ymax
S(x,y,t+1)=S(x,y,t)
165 Continue
160 Continue
! gCの値から成長する点を選ぶ
do 60 x=1,xmax
do 65 y=1,ymax
if ((gC(x,y,t)/gCmax)**2>=(rand(t))/5) S(x,y,t+1)=S(x,y,t+1)+1
65 Continue
60 Continue
! ★1回の判定終わり
! ◆data書き込み
write (fname,'(a,i4.4,a)') 'dendrite',t,'.dat'
open (10, file=fname, status='replace')
Do 98 x=1,xmax
Do 97 y=1,ymax
if (S(x,y,t) >= 1) write(10, *) x , y
97 Continue
98 Continue
close(10)
99 Continue
end program main
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
出来上がったdatファイルをまずはgnuplotでpngに、それをフリーソフトのGiamでつないでGIFアニメーションの作成をします。
そのために、以下の様なgplファイルをまず作成します。
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
set xrange [1:200]
set yrange [1:200]
set terminal png
set output "0.png"
set output "0.png"
plot "denderite_0001.dat" title "" lt 1 lw 4
set output "1.png"
plot "denderite_0002.dat" title "" lt 1 lw 4
set output "2.png"
plot "denderite_0003.dat" title "" lt 1 lw 4
set output "3.png"
plot "denderite_0004.dat" title "" lt 1 lw 4
set output "4.png"
plot "denderite_0005.dat" title "" lt 1 lw 4
set output "5.png"
plot "denderite_0006.dat" title "" lt 1 lw 4
set output "6.png"
～中略～
plot "denderite_0076.dat" title "" lt 1 lw 4
set output "76.png"
plot "denderite_0077.dat" title "" lt 1 lw 4
set output "77.png"
plot "denderite_0078.dat" title "" lt 1 lw 4
set output "78.png"
plot "denderite_0079.dat" title "" lt 1 lw 4
set output "79.png"
plot "denderite_0080.dat" title "" lt 1 lw 4
set output "80.png"
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
これをターミナルから読み込ませます。gplファイルとdatファイルの両方が置いてあるディレクトリに移動し、「gnuplot ファイル名.gpl」と入力すれば、png画像が生成されます。
そして、先ほど紹介したフリーソフトでつなぎ合わせると、以下の様なGIFによる結晶成長アニメーションが作成出来ます。
その他、おまけとして境界条件や乱数の大きさを変えたものの最終状態の画像だけ載せてみます。
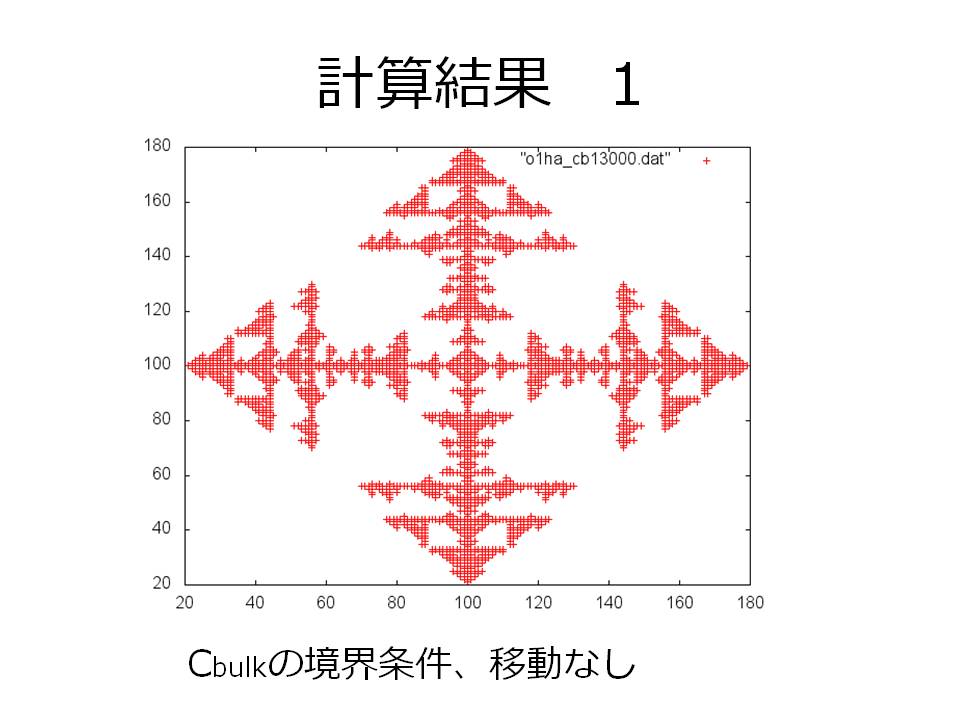
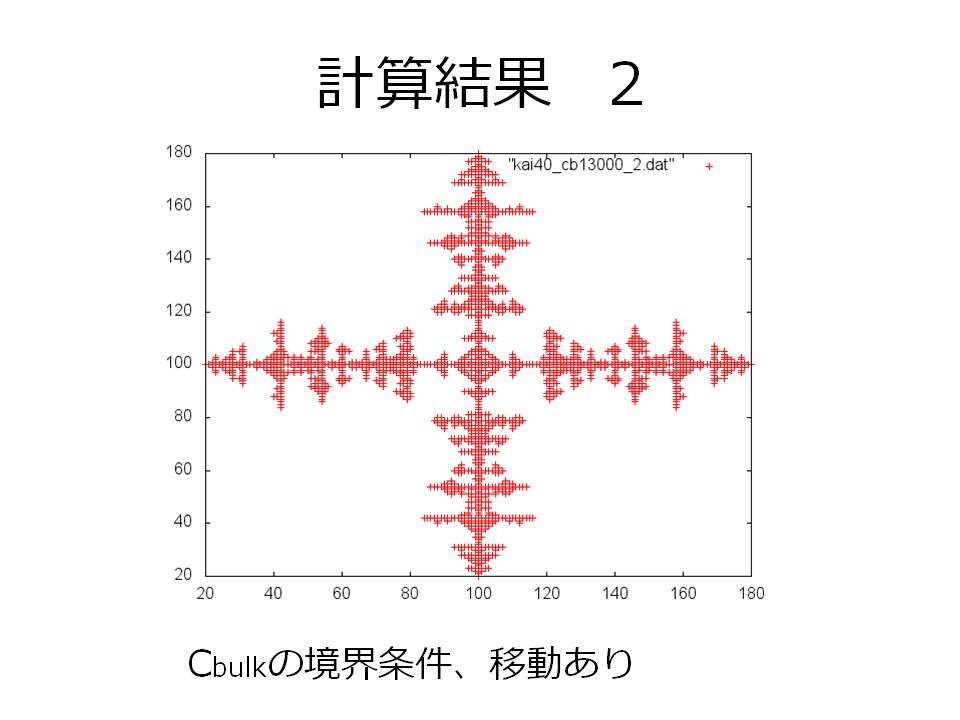
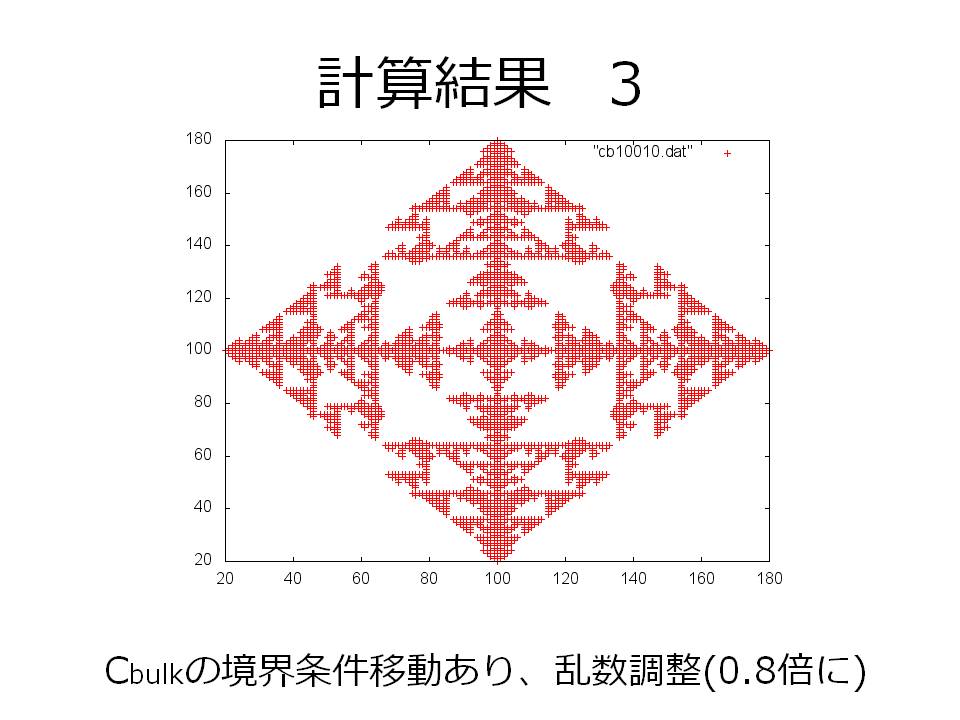
重大なミスなのですが、当初予想していた「過飽和度の変化による結晶成長の変化」が何故か再現できず、CbulkとCsatの組合せをどう変えてもほとんど同じ結晶の形が現れるプログラムとなってしまいました。本当に純粋に拡散律速の部分だけをプログラムしてしまったためでしょうかね。もう少し他の物理を入れれば、樹枝状結晶の枝ぶりの変化やもしかしたら骸晶や球晶などの再現もできたかもしれません。
とまぁ、考察みたいにしてまとめて、授業の発表はやりましたw(数値演習の授業では、自由課題をFortranでプログラムして、その結果を全員で発表するというものを毎年やってるのですw)
しかし実際には、当然私ごときが言うまでもなく十分な研究がされており、フェーズフィールド法Phase Field Method(PFM)というものがあります。詳しくは以下のリンクや書籍を参考にしてみて下さい。
・大規模GPU計算によるフェーズフィールド法によるAl-Si合金の樹枝状凝固成長シミュレーション(東工大青木研究室、美しい動画付きなのでゼヒ！)
・京都大学計算科学ユニット2012年度第2回研究交流会「工学における計算科学の展開」より(フェーズフィールド法の数式などの解説が載ってます)